Roulette Color Probability
Except for the zero (single and double) which has the color green, the numbers in roulette are basically divided into two types – those that are colored red and those that are black. In roulette, you can make bets based on these colors. This kind of bet is called the Color Bet. In this bet, the players would only have to predict whether the next spin will result to a Red or Black number.
Focusing of European Roulette, the odds that your colour will not hit for 10 rounds in a row is 1 to 784. This might seem good, but keep in mind that the odds are like this only at the start of the game. Probability, the Martingale system and the 'delayed' double-up betting strategy. At roulette each spin is a new spin and the outcome is never determined by prior spins. After eight successive blacks, a black is as likely to come up as a red. You may argue that the reds and blacks will eventually even out over a long run, and you would be right. There are several ways to bet on roulette and it is also affected by probability. A player do a single number bet or bet on a color, odd/even and high and low. Single number bets only have a 2.63% chance of winning, while color bets and the rest have a 43.67% of chance of winning.
Roulette Color Bet Odds. So, what is the probability that a red ball will appear most? Let’s assume that you are playing on a European roulette wheel. The odds of red appearing here are 18 over 37 or 1 in 2.06.
The Color Bet field in the roulette betting layout can be found labelled in its respective color. Just like in this image below:
Since this is an outside bet, the payoff for a Color Bet is 1 to 1. This means that, for example, your £1 will win another £1. Depending on the casino, the zeros are not oftentimes not included in the colored bet.
What makes this bet quite popular, especially among beginners, is that it’s so easy to carry out and there’s no need to think that much. A player only has to choose between red or black.
Furthermore, you don’t have to bother yourself as to what number came up. In an online roulette casino, you just have to look at the color of the pocket to where the ball lands.
Chances of Winning
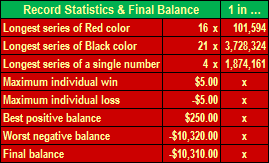
Betting in Red or Black is a great way to play and win in roulette. In this setup, the player’s chance of winning a spin is almost 50/50. Note: it is said “almost†because we cannot discount the casino advantage (which is the single and double zero). This means that if the ball falls on either of the zeros, you would lose no matter which color you chose.
For exact figures, the odds of winning in a European roulette when betting on colors are 48.64%. In the American roulette, the player’s chance is smalle at 47.36%. Still, both figures are quite impressive.
How to Bet in Colors
As already stated, Betting in Colors is very easy. Perhaps this is as simple as betting on Odd or Even. All of you have to do is device which color you would like to put your chips. Here’s the breakdown of the numbers:

- There are 8 even and 10 odd numbers in Red
- There are also 8 even and 10 odd numbers in Black
- 0 and 00 are green
Strategies to Pair With
Betting in Colors is by itself, quite effective. However, if you want to maximize further your profits, you can use even money bet systems like this or this.
Successful Color Bets in History
One of the most famous color bets made in the history of the game was done by Ashley Revell. In 2004, he left London and flew to Vegas with everything he has worth £135,000. To say that this is a high-risk gambling journey would be an understatement. It’s a one-way trip because he already got no place to return to should he lose.
The whole world held its breath (the game was televised) as he put all that he had on black. In a sudden change of heart, he pushed his chips to Red. The ball landed on 7, which is a red. All of a sudden, Mr. Revell doubled everything he has and went home a happy man.
Problem: A spinner has 4 equal sectors colored yellow, blue, green and red. What are the chances of landing on blue after spinning the spinner? What are the chances of landing on red?
Solution: The chances of landing on blue are 1 in 4, or one fourth.
The chances of landing on red are 1 in 4, or one fourth.
This problem asked us to find some probabilities involving a spinner. Let's look at some definitions and examples from the problem above.
| Definition | Example |
| An experiment is a situation involving chance or probability that leads to results called outcomes. | In the problem above, the experiment is spinning the spinner. |
| An outcome is the result of a single trial of an experiment. | The possible outcomes are landing on yellow, blue, green or red. |
| An event is one or more outcomes of an experiment. | One event of this experiment is landing on blue. |
| Probability is the measure of how likely an event is. | The probability of landing on blue is one fourth. |
In order to measure probabilities, mathematicians have devised the following formula for finding the probability of an event.
| Probability Of An Event | |||
|
The probability of event A is the number of ways event A can occur divided by the total number of possible outcomes. Let's take a look at a slight modification of the problem from the top of the page.
Experiment 1: A spinner has 4 equal sectors colored yellow, blue, green and red. After spinning the spinner, what is the probability of landing on each color?
The possible outcomes of this experiment are yellow, blue, green, and red.
Probabilities:
| P(yellow) | = | # of ways to land on yellow | = | 1 |
| total # of colors | 4 | |||
| P(blue) | = | # of ways to land on blue | = | 1 |
| total # of colors | 4 | |||
| P(green) | = | # of ways to land on green | = | 1 |
| total # of colors | 4 | |||
| P(red) | = | # of ways to land on red | = | 1 |
| total # of colors | 4 |
Experiment 2: A single 6-sided die is rolled. What is the probability of each outcome? What is the probability of rolling an even number? of rolling an odd number?
Outcomes: The possible outcomes of this experiment are 1, 2, 3, 4, 5 and 6.
Probabilities:
| P(1) | = | # of ways to roll a 1 | = | 1 | ||
| total # of sides | 6 | |||||
| P(2) | = | # of ways to roll a 2 | = | 1 | ||
| total # of sides | 6 | |||||
| P(3) | = | # of ways to roll a 3 | = | 1 | ||
| total # of sides | 6 | |||||
| P(4) | = | # of ways to roll a 4 | = | 1 | ||
| total # of sides | 6 | |||||
| P(5) | = | # of ways to roll a 5 | = | 1 | ||
| total # of sides | 6 | |||||
| P(6) | = | # of ways to roll a 6 | = | 1 | ||
| total # of sides | 6 | |||||
| P(even) | = | # ways to roll an even number | = | 3 | = | 1 |
| total # of sides | 6 | 2 | ||||
| P(odd) | = | # ways to roll an odd number | = | 3 | = | 1 |
| total # of sides | 6 | 2 |
Experiment 2 illustrates the difference between an outcome and an event. A single outcome of this experiment is rolling a 1, or rolling a 2, or rolling a 3, etc. Rolling an even number (2, 4 or 6) is an event, and rolling an odd number (1, 3 or 5) is also an event.
In Experiment 1 the probability of each outcome is always the same. The probability of landing on each color of the spinner is always one fourth. In Experiment 2, the probability of rolling each number on the die is always one sixth. In both of these experiments, the outcomes are equally likely to occur. Let's look at an experiment in which the outcomes are not equally likely.
Experiment 3: A glass jar contains 6 red, 5 green, 8 blue and 3 yellow marbles. If a single marble is chosen at random from the jar, what is the probability of choosing a red marble? a green marble? a blue marble? a yellow marble?
Outcomes: The possible outcomes of this experiment are red, green, blue and yellow.

Probabilities:
| P(red) | = | # of ways to choose red | = | 6 | = | 3 |
| total # of marbles | 22 | 11 | ||||
| P(green) | = | # of ways to choose green | = | 5 | ||
| total # of marbles | 22 | |||||
| P(blue) | = | # of ways to choose blue | = | 8 | = | 4 |
| total # of marbles | 22 | 11 | ||||
| P(yellow) | = | # of ways to choose yellow | = | 3 | ||
| total # of marbles | 22 |
The outcomes in this experiment are not equally likely to occur. You are more likely to choose a blue marble than any other color. You are least likely to choose a yellow marble.
Experiment 4: Choose a number at random from 1 to 5. What is the probability of each outcome? What is the probability that the number chosen is even? What is the probability that the number chosen is odd?
Outcomes: The possible outcomes of this experiment are 1, 2, 3, 4 and 5.
Probabilities:
| P(1) | = | # of ways to choose a 1 | = | 1 |
| total # of numbers | 5 | |||
| P(2) | = | # of ways to choose a 2 | = | 1 |
| total # of numbers | 5 | |||
| P(3) | = | # of ways to choose a 3 | = | 1 |
| total # of numbers | 5 | |||
| P(4) | = | # of ways to choose a 4 | = | 1 |
| total # of numbers | 5 | |||
| P(5) | = | # of ways to choose a 5 | = | 1 |
| total # of numbers | 5 | |||
| P(even) | = | # of ways to choose an even number | = | 2 |
| total # of numbers | 5 | |||
| P(odd) | = | # of ways to choose an odd number | = | 3 |
| total # of numbers | 5 |
The outcomes 1, 2, 3, 4 and 5 are equally likely to occur as a result of this experiment. However, the events even and odd are not equally likely to occur, since there are 3 odd numbers and only 2 even numbers from 1 to 5.
Roulette Color Probability Definition
Summary: The probability of an event is the measure of the chance that the event will occur as a result of an experiment. The probability of an event A is the number of ways event A can occur divided by the total number of possible outcomes. The probability of an event A, symbolized by P(A), is a number between 0 and 1, inclusive, that measures the likelihood of an event in the following way:
- If P(A) > P(B) then event A is more likely to occur than event B.
- If P(A) = P(B) then events A and B are equally likely to occur.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | Which of the following is an experiment? |
| 2. | Which of the following is an outcome? |
| 3. | Which of the following experiments does NOT have equally likely outcomes? |
| 4. | What is the probability of choosing a vowel from the alphabet? |
Roulette Color Probability Games
| 5. | A number from 1 to 11 is chosen at random. What is the probability of choosing an odd number? |